图论算法记录

主要以有向加权图为主，涉及到 图的几种常见表示方法、拓扑排序、弗洛伊德算法(Floyd)算法、 狄克斯特拉(dijkstra)算法、 SPFA算法、贝尔曼-福特(Bellman-Ford)算法

图的常见表示方法

1. 邻接矩阵：

2. 邻接表：

3. 边缘列表

在刷题的时候经常以这种形式给出，可以将其转换乘邻接表或者邻接矩阵

完整

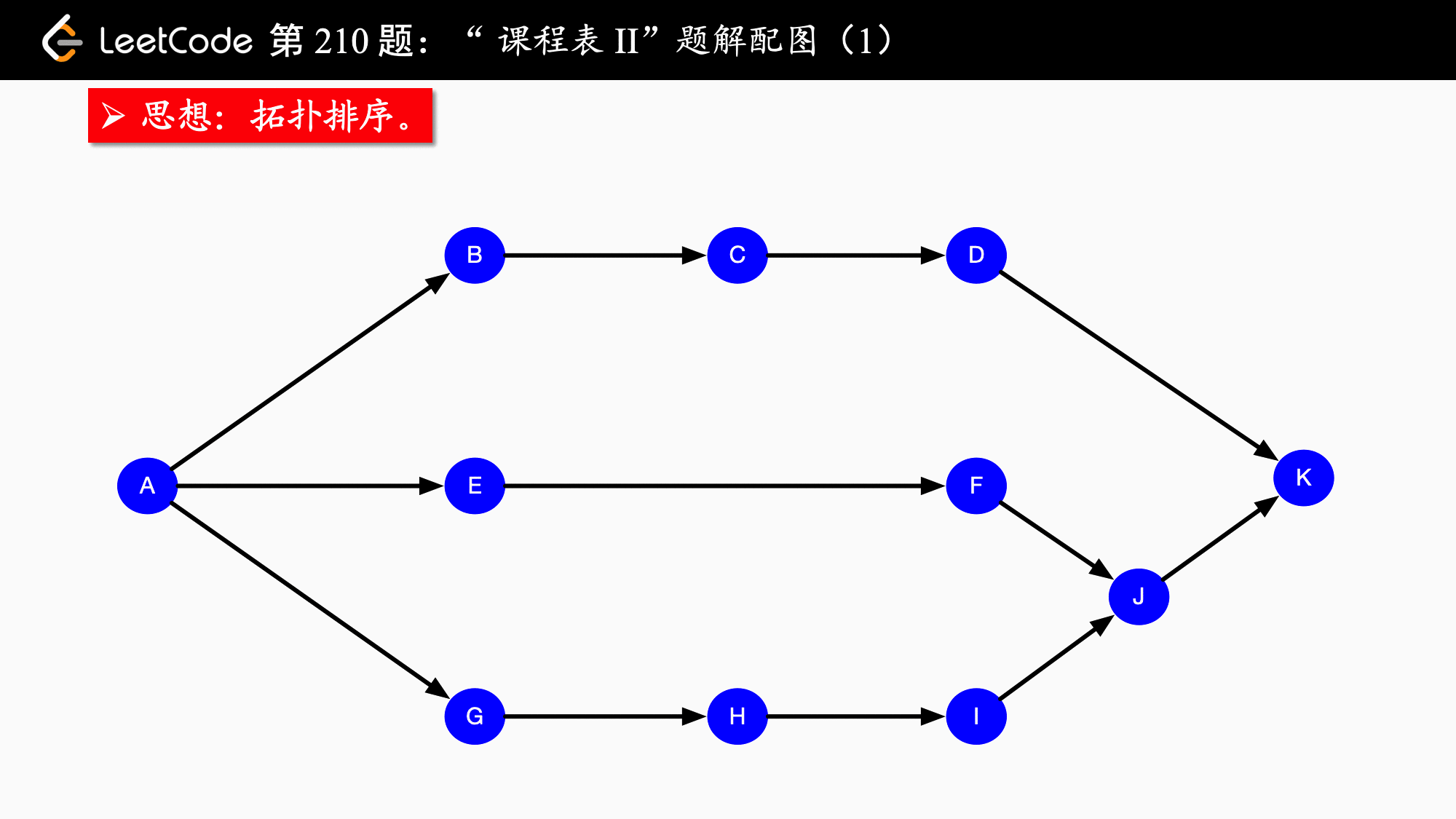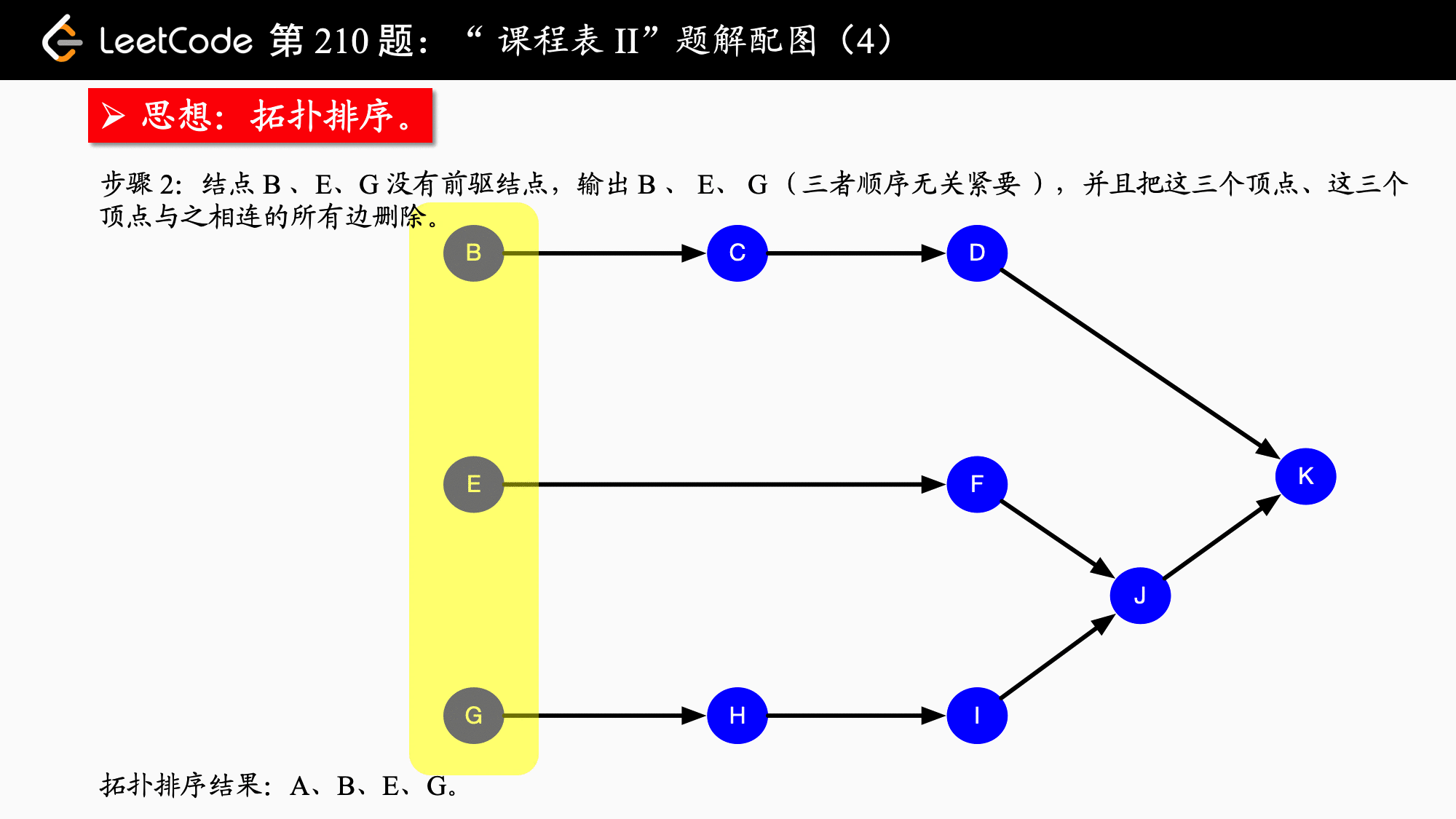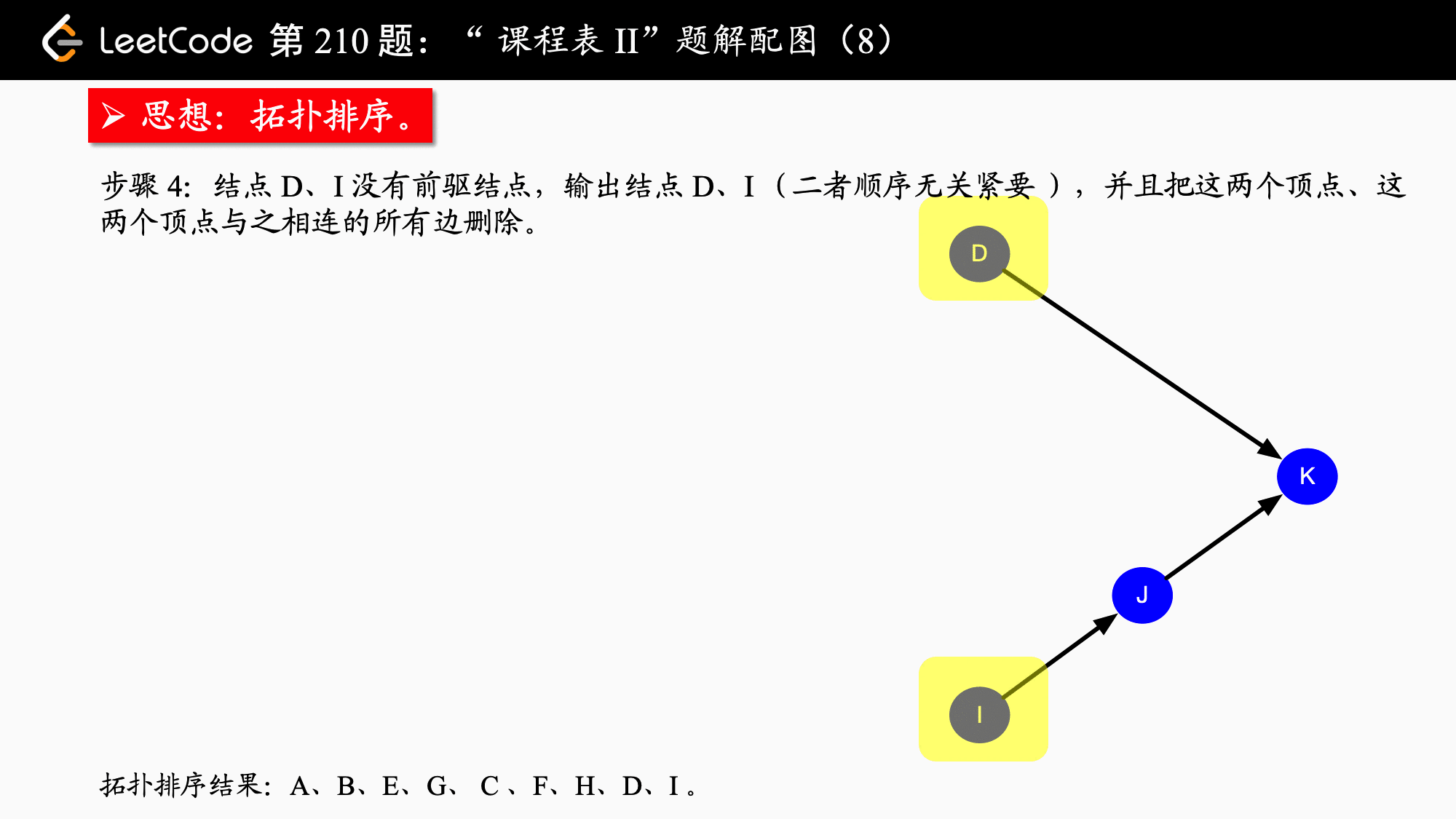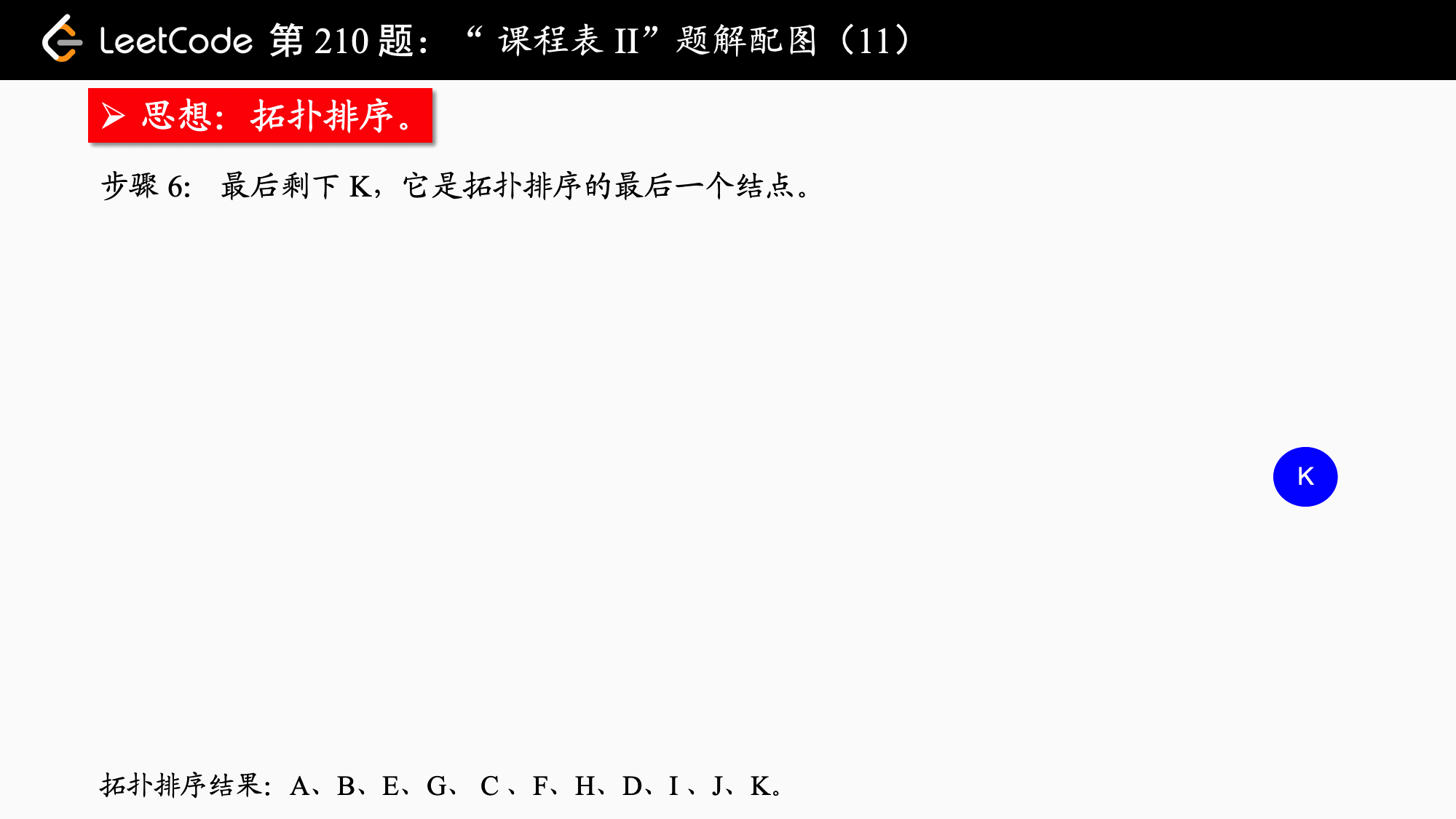
拓扑排序

其简单思路就是先找到入度为0 的节点，并将该节点放入队列中，同时将与他相邻的节点的入度减一，以此往复，如果最后所有节点的入度都为零则说明可以完成拓扑排序，否则该图不能进行拓扑排序

具体的算法流程如下：

在算法开始前，扫描对应的存储空间(使用邻接表)，将入度为 0 的节点放入队列中
只要队列非空，就从队首取出入度为0 的节点，并且将这个结点的所有邻接结点（它指向的结点）的入度减1，在减 1 以后，如果这个被减 1 的结点的入度为 0 ，就继续入队。
队列为空时，检查结果集是否满足要求

除了需要保存入度为0 的队列，还需要两个辅助的数据结构：

1). 邻接表：通过节点的索引，能够得到这个节点的后继节点；

2). 入度数组：通过节点的索引能够得到指向这个节点的节点个数

leetcode207 课程表

题目描述：

现在你总共有 n 门课需要选，记为 0 到 n-1。

在选修某些课程之前需要一些先修课程。例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示他们: [0,1]

给定课程总量以及它们的先决条件，判断是否可能完成所有课程的学习？

示例 1:

1
2
3

输入: 2, [[1,0]] 
输出: true
解释: 总共有 2 门课程。学习课程 1 之前，你需要完成课程 0。所以这是可能的。

示例 2:

1
2
3

输入: 2, [[1,0],[0,1]]
输出: false
解释: 总共有 2 门课程。学习课程 1 之前，你需要先完成课程 0；并且学习课程 0 之前，你还应先完成课程 1。这是不可能的。

来源：力扣（LeetCode）

链接：https://leetcode-cn.com/problems/course-schedule

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

解题

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

bool canFinish(int numCourses, vector<vector<int>>& prerequisites) { 
    //输入prerequisites是边缘列表
    int clen = prerequisites.size(); //课程的长度
    if (clen == 0)
        return true; // 课程长度为零，所以肯定可以学习完
    //1.初始化入度的数组 和 邻接表数组
    vector<int> indegree(numCourses); //入度数组，初始化为0
    vector<vector<int>> adj(numCourses); //邻接表数组
    for (int i = 0; i < clen; ++i) {
        indegree[prerequisites[i][0]] += 1;  //统计每个顶点的度
        adj[prerequisites[i][1]].push_back(prerequisites[i][0]); // 创建邻接表
    }
    //2. 创建队列，在拓扑排序之前，将所有入度为0的顶点存入队列中
    queue<int> myqueue;
    for (int i = 0; i < indegree.size(); ++i) {
        if (indegree[i] == 0)
            myqueue.push(i);
    }
    // 3. 开始拓扑排序，主要是遍历前面的邻接表，然后找到表中顶点对应的入度，对入度减一操作，若检测到入度为0时则推入队列中，准备输出（删除）
    int count = 0;
    while (!myqueue.empty()) {
        ++count;
        int top = myqueue.front(); // 得到首元素
        myqueue.pop();  //删除首元素
        //vector<int> tmp = adj[top];
        for (vector<int>::iterator iter = adj[top].begin(); iter != adj[top].end(); ++iter) {
            --indegree[*iter];
            if (indegree[*iter] == 0)
                myqueue.push(*iter);
        }
    }
    return count == numCourses;
}

leetcode210 课程表2

和前面一样不同的是需要把课程表输出


vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisities) {
    vector<int> res;
    //1. 初始化入度数组和邻接表'
    if (prerequisities.size() == 0) {  // 如果prerequisities大小为零，没有特别说明课程完成的先后顺序，则所有课程都能完成
        while(numCourses >0)
            res.push_back(--numCourses);
        return res;
    }

    vector<int> indegree(numCourses); //入度数组
    vector<vector<int>> adj(numCourses); //邻接表数组
    for (int i = 0; i < prerequisities.size(); ++i) {
        indegree[prerequisities[i][0]] += 1;  // 入度+1
        adj[prerequisities[i][1]].push_back(prerequisities[i][0]); // 扩展邻接表
    }
    //2. 创建队列，将度为0的元素推入队列中
    
    queue<int> Myqueue;
    for (int i = 0; i < indegree.size(); ++i) {
        if (indegree[i] == 0)
            Myqueue.push(i);
    }

    //3. 统计每个顶点的度，判断是否为零，减一和push进入队列中
    while (!Myqueue.empty()) {
        int top = Myqueue.front();
        res.push_back(top);
        Myqueue.pop();
        for (vector<int>::iterator iter = adj[top].begin(); iter != adj[top].end(); ++iter) {
            --indegree[*iter];
            if (indegree[*iter] == 0)
                Myqueue.push(*iter);
        }
    }
    if (res.size() != numCourses)
        res = {};  // 输出空数组
    return res;
}

弗洛伊德算法(Floyd)

弗洛伊德算法是经典的 多源最短路径 算法，可以正确处理有向图或有向图的负权，但不可存在负权回路的最短路径问题，同时也被用于计算有向图的传递闭包。

大概思路：

定义两个二维矩阵D和P， D记录顶点间的最小路径，P记录顶点间最小路径中的中转点
通过三重循环，k为中转点，v为起点，w为终点，循环比较D[v][w] 和 D[v][k]+D[k][w]最小值，如果后者更小则替换前者

具体：

矩阵 D 记录顶点间的最小路径
例如 D[0][3]= 10，说明顶点 0 到 3 的最短路径为 10；
矩阵 P 记录顶点间最小路径中的中转点
例如 P[0][3]= 1 说明，0 到 3 的最短路径轨迹为：0 -> 1 -> 3。
它通过 3 重循环，k 为中转点，v 为起点，w 为终点，循环比较 D[v][w] 和 D[v][k] + D[k][w]最小值，如果 D[v][k] + D[k][w] 为更小值，则把 D[v][k] + D[k][w] 覆盖保存在 D[v][w]中。

步骤演示：

图片来源

leetcode743 网络延迟时间

输入： times[i] = (u,v,w)，分别表示源节点、目标节点、它们之间的传递时间； N：网络节点的个数， K表示测试时的起始节点
范围： N:[1,100], K:[1,N], times:[1,6000], 1 <= u,v<= N ,0 <= w <= 100
输出：如果可以使所有节点都收到信号则返回总的时间，如果不能则返回-1

int networkDelayTime_Floyd(vector<vector<int>>& times, int N, int K) {
    //创建二维稀疏矩阵表示 ==> 邻接矩阵
    vector<vector<int>> v(N + 1, vector<int>(N + 1, -1)); // 创建二维vector 并初始化为-1表示永远不会到达
    //填充邻接矩阵
    for (int i = 1; i <= N; ++i) {
        v[i][i] = 0;
    }
    for (int i = 0; i < times.size(); ++i) {
        v[times[i][0]][times[i][1]] = times[i][2];
    }
    //接下来进入Floyd算法的三重循环
    for (int k = 1; k <= N ; ++k) {  //这里的小k表示的就是中间节点，尝试使用每个中间节点进行替换
        for (int i = 1; i <= N; ++i) {
            for (int j = 1; j <= N; ++j) {
                //当满足下面的条件时，使用中间节点进行替换
                //1. 中间节点不为-1，即i -> k 和 k -> j 这条有向边是存在的
                //2. 在满足条件1 的基础上，经过中间节点花费的时间可以比原来小，或者 原来的有向边不存在
                if (v[i][k] != -1 && v[k][j] != -1 && (v[i][j] > v[i][k] + v[k][j] || v[i][j] == -1))
                    v[i][j] = v[i][k] + v[k][j];
            }
        }
    }
    //通过上面的三重循环，就将每个节点之间的最短通路找到了（如果存在的话）
    int res = -1;
    //因为最后的结果是要返回从该节点K出发遍历所有节点所花费的时间
    //所以首先判断是否为-1以此判断K是否可以联通所有节点，如果存在存在-1说明此路不通直接返回-1；
    //否则，将最大的那个值输出，因为最大值表示从K出发经过了所有的节点累加得到的路径长度，符合最后的要求
    for (int i = 1; i <= N; ++i) {
        if (v[K][i] == -1)
            return -1;  //说明这个节点是走不通的
        res = max(res, v[K][i]); 
    }
    return res;
}

狄克斯特拉算法(Dijkstra)

最经典的 单源最短路径 (一个点到其余各个顶点的最短路径)算法，适用于边权为正的无向和有向图，不适用于有负边权的图.

基本思想：

每次找到离源点最近的一个顶点，然后以该顶点为中心进行扩展，最终得到源点到其余所有点的最短路径。

基本步骤：

将所有顶点分为两部分：已知最短路程的顶点集合P和未知最短路程的顶点集合Q。最开始，已知最短路径的顶点集合P中只有源点一个顶点。这里使用一个book[i]数组来记录哪些点在集合P中。例如对于某个顶点i，如果book[i]=1则表示这个顶点在集合P中，book[i]=0则表示这个顶点在集合Q中；
设置源点s到自己的最短路径为0即dis=0。若存在源点能直接到达顶点i，则把dis[i]设为e[s][i]，同时把所有其它（源点不能直接到达的）顶点的最短路径设置为 $ \infty$；
在集合Q的所有顶点选择一个离源点s最近的顶点u（即dis[u]最小）加入到集合P。并考察所有以点u为起点的边，对每一条边进行松弛操作。例如存在一条边从 u到v的边，那么可以通过将边 u -> v添加到尾部来拓展一条从s 到v的路径，这条路径的长度是 dis[u]+e[u][v]，如果这个值比目前已知的dis[v]的值要小，可以用这个新值代替dis[v]中的值；
重复第三步，如果集合Q为空，算法结束。最终dis 数组中的值就是源点到所有顶点的最短路径。

步骤演示：

给出下图：

创建邻接矩阵：

使用一个一维数组dis存储1号顶点到其余各个顶点的初始路程:

找到离1号顶点最近的顶点，首先就是其本身，因为其操作没有特殊性，直接参考后续步骤。然后找到的最近顶点为2，然后查看2号顶点的出边有： 2->3, 2->4这两条边。先讨论2->3这条边能否让1号顶点到3号顶点的路程变短，也就是比较dis[3] 和 dis[2] + e[2][3]的大小，发现 12 > 1+9，所以dis[3]更新为10,同理分析 2->4这条边， dis[4] = $ \infty$ > dis[2] + e[2][4] = 4 所以dis[4] = 4，dis更新如下：

继续在 3,4,5,6顶点中查找离1号顶点最近的点，发现是4号顶点，其出边为 4->3, 4->5, 4->6。

1
2
3

对于4 ->3 ,dis[3] = 10 > dis[4] + e[4][3] = 8,故 dis[3]更新为8;
对于4->5, dis[5] = inf > dis[4] + e[4][5] = 17, 故 dis[5] = 17;
同理 dis[6] = 19

所以dis更新如下：

继续在3,5,6中查找离1号顶点最近的点，发现是3号顶点，其出边为 3->5。

1	3 -> 5， dis[5] = 17 > dis[3] + e[3][5] = 13，故dis[5] = 13

所以dis更新如下：

（图中6号节点对应的19，背景应该是白色的）

继续在5,6中查找，最近点为5，其出边为 5->6：

1	5->6, dis[6] = 19 > dis[5] + e[5][6] = 17，dis[6] = 17

最后对顶点6进行松弛，发现没有出边故不处理，最终dis数组如下，这便是1号顶点到其余各个顶点的最短路径：

参考

leetcode743 网络延时时间

前面使用了Floyd算法求解，这里使用Dijkstra算法求解：

int networkDelayTime_Dijkstra(vector<vector<int>>& times, int N, int K) {
    //创建邻接矩阵
    vector<vector<int>> v(N + 1, vector<int>(N + 1, -1)); //使用-1代替无穷大值，可能会有些许麻烦，之后尝试替换为 MAX_INT
    for (int i = 0; i < times.size(); ++i) {
        v[times[i][0]][times[i][1]] = times[i][2];
    }
    vector<int> S(N + 1, -1), T(N + 1, -1); //S为确定数组，T为估计数组
    //根据单源节点填充数组
    for (int i = 1; i < N + 1; ++i) {
        if (v[K][i] != -1)
            T[i] = v[K][i];
    }
    T[K] = 0;
    //找到距离单元节点最短距离的节点
    int minVal = -1,minIndex = -1;
    for (int c = 0; c < N; ++c) {
        minVal = -1;
        for (int i = 1; i < N + 1; ++i) {
            if (T[i] != -1 && S[i] == -1) {
                if (minVal == -1 || T[i] < minVal) {
                    minVal = T[i];
                    minIndex = i;
                }
            }
        }
        S[minIndex] = minVal; // 确定值
        // 以这个节点(minIndex)出发，找到其每个出边，并和原始距离进行比较，更新数组 T(估计数组)
        for (int i = 1; i < N + 1; ++i) {
            if (v[minIndex][i] != -1 && (minVal + v[minIndex][i] < T[i] || T[i] == -1))
                T[i] = minVal + v[minIndex][i]; // 估计值
        }
    }
    int res = -1;
    for (int i = 1; i < S.size(); ++i) {
        if (S[i] == -1)
            return -1;
        res = max(res, S[i]);
    }
    return res;
}
//这里使用-1 代替了 inf ，后续尝试修改成inf

解题参考

SPFA算法

SPFA算法是 单源最短路径 算法，是Bellman-ford队列优化，和BFS的关系密切，相较于狄克斯特拉算法，边的权重可以是负数、实现简单，但是时间复杂度过高。

基本思路：

使用一个先进先出的队列保存待优化的节点，优化时每次取出队首的节点 u ，并且对于 u 的所有出边所指向的节点v进行松弛操作，如果 v 点的最短路径估计值有所调整且v 点不在当前队列中，就将 v 点放入队尾。这样不断从队列中取出节点来进行松弛操作，直至队列为空。

步骤：

leetcode743 网络延时时间


int networdDelay_SPFA(vector<vector<int>>& times, int N, int K) {
    vector<int> T(N + 1, -1);  //估计值
    vector<int> Flag(N + 1, -1);  // 用来标记节点是否在队列中
    queue<int> Myqueue;  //队列
    vector<vector<int>> v(N + 1, vector<int>(N + 1, -1));
    for (int i = 0; i < times.size(); ++i) {
        v[times[i][0]][times[i][1]] = times[i][2];
    }
    for (int i = 1; i < N + 1; ++i)
        v[i][i] = 0;
    T[K] = 0;
    Myqueue.push(K);  
    Flag[K] = 0; // 
    while (!Myqueue.empty()) {  //只要队列不为空就一直循环
        int u = Myqueue.front();
        Myqueue.pop();
        Flag[u] = -1; //此时tmp 不在队列中
        for (int i = 1; i < N + 1; ++i) {
            if (v[u][i] != -1 &&( T[i] > T[u] + v[u][i]  ||  T[i] == -1)){
                T[i] = T[u] + v[u][i];
                if (Flag[i] == -1) {//说明此时这个节点i不在队列中
                    Myqueue.push(i);
                    Flag[i] = 0;
                }
            }
        }
    }
    int res = -1;
    for (int i = 1; i < N + 1; ++i) {
        if (T[i] == -1)
            return -1;
        res = max(res, T[i]);
    }
    return res;
}

贝尔曼-福特算法(Bellman-Ford)

参考

其原理是对图进行最多n-1次松弛操作，得到所有可能的最短路径。其边的权重可以是负数，实现简单但是复杂度过高，复杂度为$O(NE)$ 其中N为顶点个数，E为边数。

基本思路：

初始化时将起点s 到各顶点v的距离dis(s->v)赋值为 $\infty$，dis(s->s)赋值为0；
后续进行最多n-1 次遍历，对所有边进行松弛操作；
遍历都结束，若再进行一次遍历，还能得到s 到某些节点更短路径的话，就说明存在负环路（负环路会随着遍历次数的增加而不断减小）

思路上与狄克斯特拉算法最大的不同是每次都是从源点s 重新出发进行 “松弛”更新操作，而狄克斯特拉算法则是从源点出发向外扩逐个处理相邻（最近）的节点。

leetcode743 网络延时时间

// 4. Bellman-Ford算法
int networdDelay_BellmanFord(vector < vector<int>>& times, int N, int K) {
    vector<int> T(N + 1, -1);
    T[K] = 0;

    for (int c = 0; c < N - 1; ++c) {
        for (int i = 0; i < times.size(); ++i) {
            int src = times[i][0], target = times[i][1], dis = times[i][2];
            if (T[src] != -1 && (T[src] + dis < T[target] || T[target] == -1)) {
                T[target] = T[src] + dis;
            }
        }
    }
    int res = -1;
    for (int i = 1; i < N + 1; ++i) {
        if (T[i] == -1)
            return -1;
        res = max(res, T[i]);
    }
    return res;

}