堆、判断2的幂次方、Python线程安全
Python的线程安全
什么是线程安全?
在一段程序中,如果两个线程t1,t2共享一个全局变量,且这多个线程对同一个全局变量操作会出现资源竞争的问题,从而导致结果会不正确,即遇到线程安全的问题。所以一般采用线程同步或互斥锁机制保证共享数据在任何时刻,最多有一个线程访问,以保证数据的正确性。
其中Python内置类型: ditc, list, tuple是线程安全的。
快速判断一个数是否是 2 的幂次方
如果将这个数减去1后会发现,仅有的那个1会变为0,而原来的那n个0会变为1;因此将原来的数与去减去1后的数字进行与运算后会发现为零。
例如:
则8(1000)就是2的幂次方。
堆
堆是一种 非线性结构 ,可以把堆看作一个数组,也可以被看作是一个 完全二叉树 (若设二叉树的深度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第 h 层所有的结点都连续集中在最左边,这就是完全二叉树。), 堆其实就是 利用完全二叉树的结构来维护的一维数组。
大顶堆: 每个节点的值都 大于或等于 其左右孩子节点的值;
小顶堆: 每个节点的值都 小于或等于 其左右孩子节点的值;
堆的这种特性非常有用,常常被当作 优先队列 使用,因为可以快速的访问到“最重要”的元素。
堆特点:

对堆中的节点按层进行编号,映射到数组中:

所以有如下堆的定义:
大顶堆:
小定顶堆:
堆排序的过程:
基本思想:
- 将待排序序列构造成一个大顶堆,此时整个序列的最大值就是堆顶的根节点。
- 将其与末尾元素进行交换,此时末尾就为最大值。
- 然后将剩余 n-1 个元素重新构造成一个堆,这样会得到 n 个元素的次小值。
- 如此反复执行,便能得到一个有序序列了,建立最大堆时是从 最后一个非叶子节点 开始从下往上调整的。
升序 — 大顶堆;
降序 — 小顶堆;
步骤一: 构造初始堆,将给定的无序序列构造成一个大顶堆:
- 给定无序序列如下:

- 从最后一个非叶子节点(
arr.length/2 -1 = 5/2-1 = 1,也就是下面的 6 节点),从左至右,从下往上进行调整:

节点6先和其左孩子比较a[2 * 1 + 1] = arr[3] =5 ,因为6 > 5所以不作调整;
和其右孩子比较a[2 * 1 + 2] = arr[4] =9, 因为 9 > 6 ,所以两者进行交换
- 找到下一个非叶子节点,当前坐标-1即 1-1 = 0,即第二个非叶子节点为4, [4,9,8]中9元素最大, 4和9 交换:

- 这时,交换导致了子根[4,5,6]混乱,继续调整,[4,5,6]中 6 最大,交换 4 和6:

步骤二:将堆顶元素和末尾元素进行交换,使末尾元素最大。然后继续调整堆,再将堆顶元素与末尾元素交换,得到第二大元素。如此反复进行交换、重建、交换:
- 将堆顶元素9 和末尾元素4 进行交换:
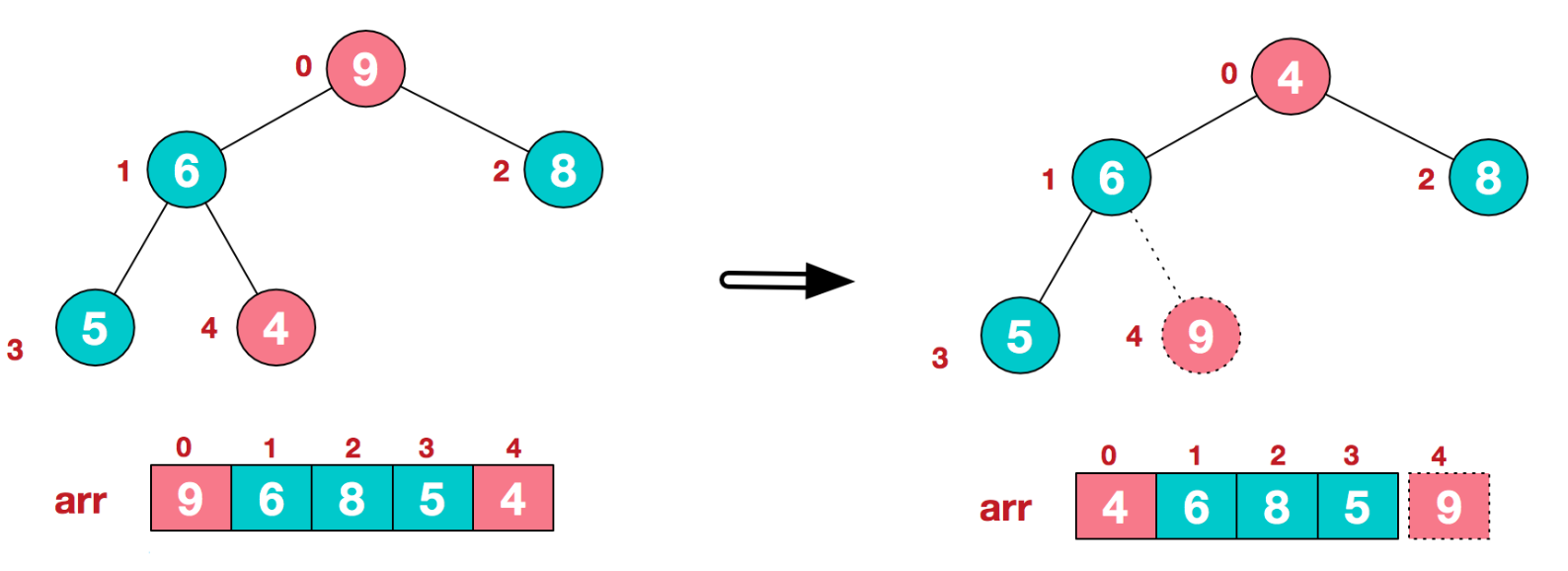
- 重新调整结构,使其继续满足堆定义:

- 再将堆顶元素 8 与末尾元素 5 进行交换,得到第二大元素8:

- 后续过程,继续进行调整、交换,如此反复,最终使得整个序列有序:

代码: