URVision

利用计算机视觉技术，对贴砖过程的进行实时校准

0. 基于视觉的UR10机器人贴砖系统

前言: 利用计算机视觉技术，对贴砖过程的进行实时校准。当前文档记录的机器人还是处在固定位置，还没有移动底座，以及视觉相关的算法。接下主要包含两个部分，一个是UR控制部分，一个是UR视觉部分。控制部分主要按照两个部分来介绍，一个是接收数据部分，接收数据部分现在是通过TCP/IP直接在Processing中读取机箱中的相关数值；另一个是机器人路径规划以及发送数据，控制机器人运动和IO相关的部分，这部分主要在Grasshopper中完成，之后也会脱离GH。

1.UR控制

UR的脚本编程语言很简单，相关文档可以参考英文文档,中文文档。在这里因为是直接利用taco，所以没有太多的涉及。

1.1读取数据

通过UR的30001或30002或30003特定的编程端口，可以与机器人控制器建立TCP/IP连接，这样我们就可以在上位机上按照URScript语言的格式编写脚本程序，直接发送给机器人控制器，机器人就可以直接执行程序了。可以参考这里，但是其中的字节顺序表是存在问题的，可以参考官方的字节顺序表。

下面给出python和java的两个例子：

python

主要先用socket读取机箱数据，然后使用struct库对获得的数据流进行解包。struct相关例子可以参考这里。简单的读取UR机箱数据例子：

import socket, math, time
import struct
HOST = "10.10.30.2"   #机箱的IP地址
PORT_30003 = 30003
joins = []
coordinates = []
while(1):
    print("start")
    try:
     s = socket.socket(socket.AF_INET, socket.SOCK_STREAM)
     s.settimeout(10)
     s.connect((HOST, PORT_30003))
     time.sleep(1.00)
     packet_1 = s.recv(12) 
     #Joint A1
     packet_3 = s.recv(8)       
     a1 = struct.unpack('!d', packet_3)[0]
     joins.append(a1) 
     #Joint A2
     packet_4 = s.recv(8)
     a2 = struct.unpack('!d', packet_4)[0]
     joins.append(a2)
     #Joint A3
     packet_5 = s.recv(8)
     a3 = struct.unpack('!d', packet_5)[0]
     joins.append(a3)
     #Joint A4
     packet_6 = s.recv(8)
     a4 = struct.unpack('!d', packet_6)[0]
     joins.append(a4)
     #Joint A5
     packet_7 = s.recv(8)
     a5 = struct.unpack('!d', packet_7)[0]
     joins.append(a5)
     #Joint A6
     packet_8 = s.recv(8)
     a6 = struct.unpack('!d', packet_8)[0]
     joins.append(a6)            
     #Skip
     packet_9 = s.recv(528)
     #X
     packet_20 = s.recv(8)
     x = struct.unpack('!d', packet_20)[0]
     x *= 1000
     coordinates.append(x)
     #Y
     packet_21 = s.recv(8)
     y = struct.unpack('!d', packet_21)[0]
     y *= 1000
     coordinates.append(y)
     #Z
     packet_22 = s.recv(8)
     z = struct.unpack('!d', packet_22)[0]
     z *= 1000
     coordinates.append(z)
     #RX
     packet_23 = s.recv(8)
     rx = struct.unpack('!d', packet_23)[0]            
     coordinates.append(rx)
     #RY
     packet_24 = s.recv(8)
     ry = struct.unpack('!d', packet_24)[0]
     coordinates.append(ry)
     #RZ
     packet_25 = s.recv(8)
     rz = struct.unpack('!d', packet_25)[0]
     coordinates.append(rz)      
     UR_Joints = joins
     UR_TCP = coordinates
     s.close()
    except:
        break
        print("Error: ")

java

这里接收数据流主要使用的是java中的DataInputStream相关函数，processing官方也给出了有关socket的介绍

//与UR建立通讯 对其进行控制
import java.io.BufferedWriter;
import java.io.IOException;
import java.io.DataInputStream;
import java.io.OutputStreamWriter;
import java.net.Socket;
import java.net.UnknownHostException;
public class URCommunication{
  String host;
  int port;
  DataInputStream is;
  OutputStream out;
  Socket s;
  ArrayList<Double> get_pose = new ArrayList<Double>();//机器人姿态数据
  ArrayList<Double> get_joint = new ArrayList<Double>(); //机器人关节位置
  int digital_output; //机器人数字输出
  float tcp_speed = 0;
  
  public URCommunication(String host){
    this.host = host;
    this.port = 30003;
    try{
      s = new Socket(host,port);
      s.setSoTimeout(2000);
      is = new DataInputStream(s.getInputStream());
      
      out = s.getOutputStream(); //向UR写数据
      
      is.skipBytes(12); //跳过前12个字节
      for(int i = 0 ; i< 6;i++){ //读取6个轴的信息
        double a = is.readDouble();
        get_joint.add(a);
      }
      
      is.skipBytes(528);
      for(int i = 0 ; i< 6;i++){ //读取姿态信息的信息
        double x;
        if(i < 3){
          x = is.readDouble() * 1000;
        }
        else{
          x = is.readDouble();
        }
        get_pose.add(x);
      }
      
      for(int i =0;i<6;i++){
        double x = is.readDouble();
        float x_f = (float)x;
        tcp_speed = tcp_speed + x_f*x_f;
      }
      tcp_speed = sqrt(tcp_speed);
      
      is.skipBytes(360); //跳过456个字节
      digital_output = (int)is.readDouble(); //得到数字输出
      
    }catch (UnknownHostException e) {
         e.printStackTrace();
   }catch (IOException e) {
         e.printStackTrace();
   }
   }

  public void closing_io(int io_num){
    String io_num_str = str(io_num);
    PrintWriter bufw=new PrintWriter(out,true);
    
    bufw.println("set_digital_out(" + io_num_str +",False)");//发送数据给服务端
    println("closing success");
  }
   
  public void closeUR(){
    try{
      s.close();
    }catch (UnknownHostException e) {
         e.printStackTrace();
   }catch (IOException e) {
         e.printStackTrace();
   }
  }
}

当然其实通过端口30003不仅可以读取数据，也是可以发送数据，以达到控制UR的效果，简单的命令基本通过发送字符串就可以实现，当然在python中还有一个URX库，可以实现对UR的控制，功能也比较齐全，之后也会使用这个库做些尝试。

1.2发送数据(机器人规划)

发送数据即为目前的控制部分，这部分主要是由Grasshopper部分完成，之后会使用python + urx完成控制路径的规划，这里主要介绍一些目前的几个部分，以及控制逻辑。
总体流程是：

• 信息初始化，生成瓷砖抓取位置，并根据一些初始化信息计算出之后每块瓷砖大概放置位置

• 放置初始瓷砖，并让机器人移动至下一个位置

• 到达指定位置后，等待接收processing发出的信号

• 接收processing的信号，进行下一步移动

1.2.1初始化

主要进行一下的一些初始化：

需要说明的是 水平方向点，该点是瓷砖水平方向上的一个点，通过人为设置，主要用来设置贴砖的方向。移动平面 高度是指机器人吸取瓷砖后在这个平面高度移动瓷砖到指定的位置。

1.2.2 生成瓷砖吸取位置

将初始吸砖位置、排列砖的列数和行数，以及砖的厚度发送到后面的 C# 代码中(代码如下)，可以得到瓷砖的排列高度。这些高度都是以点的形式存在。

List<Point3d> listPickPos = new List<Point3d>();
    int n = width * height;
    for(int i = 0; i < n; i++){
      listPickPos.Add(new Point3d(pickPos.X, pickPos.Y, pickPos.Z + (i * thickness)));
    }
    A = listPickPos;

有了这些信息，就可以在知道要贴第几块砖的情况下，告诉UR到达指定高度吸取瓷砖。

1.2.3生成放置瓷砖位置

GH中的电池如下：

简单来说就是根据在初始瓷砖的基础上，在规定的方向上，每隔一定间隔放置一块瓷砖，这个间隔由前面设置的瓷砖的宽度决定。最后就会输出一些点，这些表示每一块瓷砖应该放置的大概位置。

1.2.4由点生成路径

在得到吸取瓷砖和放置瓷砖的点集后即可以生成机器人运动路径和I/O控制命令。GH中的电池图如下：

注意 其中的number，指的是从processing获得的第几块砖的信息。有了这个信息才能准确的生成对应的放置瓷砖的位置。

该段代码目前由C#编写，如下：

private void RunScript(bool reset, List<Point3d> pickPos, DataTree<Point3d> placePos, double height, double height2, int number, ref object P, ref object O, ref object S)
  {
    int picknum = pickPos.Count;
    List<Point3d> robotPath = new List<Point3d>(); //运动路径
    List<string> io = new List<string>(); //io信号控制
    List<string> sleep = new List<string>(); //延时

    string waitTime = "1"; //电缸运动时间，用时间控制电缸的行程
    int last_index = pickPos.Count - 1; // 瓷砖的总高度
    int BranchCount = placePos.BranchCount; //放置瓷砖的brach个数,可以理解为行数
    int ListPointNum = placePos.Branch(0).Count;
    int index_row = number / ListPointNum; //判断现在是第几行
    int index_col = number % ListPointNum; //判断现在是第几列

    int count = number;  //目前贴的是第几块瓷砖

    if(!reset){
      count = 0;
      robotPath = new List<Point3d>();
    }

    if(count == 0){  //Robot Path for first pannel
      Print("HELLO FIRST PATH");
      robotPath.Add(new Point3d(pickPos[0].X, pickPos[0].Y, pickPos[0].Z + height)); //初始位置高度
      robotPath.Add(pickPos[last_index]); //到达第一个瓷砖位置位置
      io.Add("set_digital_out(3,True)"); // 电缸回收，吸取瓷砖
      sleep.Add("sleep(" + waitTime + ")"); //控制行程
      io.Add("set_digital_out(3,False)"); //电缸结束控制

      robotPath.Add(new Point3d(pickPos[0].X, pickPos[0].Y, pickPos[0].Z + height)); //回到吸瓷砖的初始高度
      robotPath.Add(new Point3d(placePos.Branch(0)[0].X, placePos.Branch(0)[0].Y, placePos.Branch(0)[0].Z + height2)); //到达放瓷砖的一个高度位置
      robotPath.Add(placePos.Branch(0)[0]); //到达放瓷砖的位置
      io.Add("set_digital_out(2,True)"); //电缸伸出，放置瓷砖
      sleep.Add("sleep(1)");
      io.Add("set_digital_out(2,False)");
      robotPath.Add(new Point3d(placePos.Branch(0)[0].X, placePos.Branch(0)[0].Y, placePos.Branch(0)[0].Z + height2)); //回到放瓷砖的一个高度位置
      robotPath.Add(new Point3d(pickPos[0].X, pickPos[0].Y, pickPos[0].Z + height));//回到吸瓷砖的初始高度
      robotPath.Add(pickPos[last_index - 1]);//到达第二块瓷砖吸取位置
      io.Add("set_digital_out(3,True)"); // 电缸回收，吸取瓷砖
      sleep.Add("sleep(" + waitTime + ")"); //控制行程
      io.Add("set_digital_out(3,False)"); //电缸结束控制

      robotPath.Add(new Point3d(pickPos[0].X, pickPos[0].Y, pickPos[0].Z + height));

      robotPath.Add(new Point3d(placePos.Branch(0)[1].X, placePos.Branch(0)[1].Y, placePos.Branch(0)[1].Z + height2));
    }

    if(count > 0 && count < pickPos.Count - 1){

      robotPath = new List<Point3d>(); //clean path
      io = new List<string>();
      sleep = new List<string>();
      Print("GOT POSITION FROM PROCESSING !!");
      io.Add("set_digital_out(2,True)"); //电缸伸出，放置瓷砖
      sleep.Add("sleep(1)");
      io.Add("set_digital_out(2,False)");

      robotPath.Add(new Point3d(placePos.Branch(index_row)[index_col].X, placePos.Branch(index_row)[index_col].Y, placePos.Branch(index_row)[index_col].Z + height2));

      robotPath.Add(new Point3d(pickPos[0].X, pickPos[0].Y, pickPos[0].Z + height));

      robotPath.Add(pickPos[last_index - count - 1]);
      io.Add("set_digital_out(3,True)"); // 电缸回收，吸取瓷砖
      sleep.Add("sleep(" + waitTime + ")"); //控制行程
      io.Add("set_digital_out(3,False)"); //电缸结束控制

      robotPath.Add(new Point3d(pickPos[0].X, pickPos[0].Y, pickPos[0].Z + height));
      if(index_col + 1 < ListPointNum){
        robotPath.Add(new Point3d(placePos.Branch(index_row)[index_col + 1].X, placePos.Branch(index_row)[index_col + 1].Y, placePos.Branch(index_row)[index_col + 1].Z + height2));
      }
      else{
        robotPath.Add(new Point3d(placePos.Branch(index_row + 1)[0].X, placePos.Branch(index_row + 1)[0].Y, placePos.Branch(index_row + 1)[0].Z + height2));
      }
    }
    if(count == pickPos.Count - 1){
      robotPath = new List<Point3d>(); //clean path
      io = new List<string>();
      sleep = new List<string>();
      Print("GOT POSITION FROM PROCESSING ,the last one!!");

      io.Add("set_digital_out(2,True)"); //电缸伸出，放置瓷砖
      sleep.Add("sleep(1)");
      io.Add("set_digital_out(2,False)");

      robotPath.Add(new Point3d(pickPos[0].X, pickPos[0].Y, pickPos[0].Z + height)); //回到吸瓷砖的初始高度
    }
    P = robotPath;
    O = io;
    S = sleep;
  }

最后会输出全部的路径点、I/O信号以及延时信号。
关于路径点，简单来说可以分成两个部分，一个部分是贴第一块瓷砖的路径，包含10个点；另一个部分是放下瓷砖后回去取下一个瓷砖并达到指定拍摄位置的路径，这中间包含5个点。

第一部分

初始位置是处于较高处的一个平面，最后会停留在第二块瓷砖放置位置的上方进行拍照获得特征信息，由特征信息对机器人姿态进行纠正，到达放置位置，等待放置瓷砖的信号.

接收到放置瓷砖的信号后，机器人末端工具头就会放下瓷砖，然后进入第二部分。

第二部分

放下瓷砖后，机器人会先进行太高，然后吸取第二块瓷砖，最后到达下一块瓷砖放置位置的上方。

之后的每一块瓷砖的放置都是循环第二部分。

1.2.5接收Processing数据

在接收processing数据部分，目前是设置了两个端口，一个端口用来接收瓷砖的纠正数据，该数据用来旋转或平移瓷砖以达到贴合的目的，但 注意 此时的瓷砖还是吸住未放下的状态。另一个端口就是用来接收使吸盘放下瓷砖的信号，同时该信号也包含了该瓷砖的为第几块瓷砖的信息。

纠正数据 主要包含一下信息：

1. 贴近类型(type)

在之前的多次测试中发现，如果两块瓷砖在相对合适（不是很近也不是很远）的位置进行拍照与靠近时可以达到比较好的效果，所以在这里，会现在processing中判断是否满足条件，如果满足则机器人可以直接贴近，如果不满足则可以适当保持一定的距离。这里使用的盘算条件如下：

if((coord_offset_left < 5.2) & (coord_offset_right < 0.6) & (angle_delta_real < 0.4) & (coord_offset_left > 1)){
          send_data_auto(1);  //说明位置正确可以靠近
        }
        else{
          send_data_auto(2);  //距离较远 先靠近一点
        }

1. UR机器人当前位置信息(robot_pose)

机器人位置信息（X,Y,Z,RX,RY,RZ）现在是由processing通过TCP/IP实时地从机箱读取,有了该信息，机器人就可以在该信息的基础上进行运动。

1. 角度偏差(angle_delta_real)

在processing中计算得到两块瓷砖的边缘直线的角度偏差，将角度偏差发送给机器人使其纠正，使两块瓷砖尽量保持平行。目前，无论是哪一种位置类型，都是计算y方向的边缘直线方程，以使该边缘平行。

1. 左拐点位置信息(corner_coord_left)

左拐点就是表示UR末端工具头吸取的那块瓷砖的角点。

1. 右拐点位置信息(corner_coord_right)

右拐点指的时前一块已经放置好的瓷砖的角点，该点就是瓷砖贴合时的参考点。

1. 右拐点参考点位置信息(corner_right_refer)

因为需要使瓷砖和瓷砖之间保持间隙，所以间隙的方向就由该点确定，只需要根据前面算出来的边缘直线就可以计算出参考点的信息。

放置信号 主要包括以下部分：

这部分主要包含当前瓷砖的数量(number)信息，因为目前图像识别部分和机器人规划部分是分别由processing和GH组成，所以需要在processing中对贴瓷砖的次数进行计数，当得到该信号后就表示机器人应该将瓷砖放下并取下一块瓷砖。

1.2.6贴砖策略

整个贴砖策略流程图如下：

现在放置瓷砖的信号是通过图像来判断，通过点击相关按钮实现瓷砖的放置。

1.2.7 I/O说明

目前使用的I/O口有：

io4: 用来打开和关闭相机
io2: 电缸伸出，放置瓷砖
io3：电缸回收，吸取瓷砖

在C#中写好何时伸出电缸，何时放置电缸的程序。

2.UR视觉

该部分主要又两部分组成，一个是手眼标定部分，一个是图像处理部分。

2.1 手眼标定

机器人的运动控制实际上是基于其基座(base)坐标下的点坐标来进行的，所以当相机采集到图像后，需要将图像上的点转换到世界坐标下才可以使机械臂到达指定位置。他们之间的转换涉及到多个转换矩阵，其中最关键的就是工具头末端和相机之间的转换矩阵，也称为手眼转换矩阵。

手眼标定(Hand-eye claibration problem)，可以分为两种情况:局部手眼，全局手眼。

局部手眼(eye-in-hand)：也叫随动手眼,相机随着机器人末端进行移动；

全局手眼(eye-to-hand)：也叫固定手眼，相机是不动的，观察机器人移动。

因为在这里，机器人位于移动底盘上，所以相机必须要跟着机器人一起移动，所以采用 局部手眼(eye-in-hand) 的方式。

2.1.1 转换矩阵的确定

主要是三个转换矩阵：

注意：下面讲到的所有世界坐标系都是指UR机器人的的基座坐标系。

1. 末端工具头坐标系到世界坐标系的转换矩阵。
2. 相机坐标系到像素坐标系之间的转换矩阵。
3. 相机坐标系到末端工具头坐标系之间的转换矩阵。

末端工具头坐标系到世界坐标系转换矩阵($H^{-1}_{rg}$)

下标中的r就表示机器人世界坐标系，g表示末端工具头坐标系

这一部分的转换矩阵不需要进行标定，只需要读取末端工具头的位置信息，在这里UR的工具头末端信息是X,Y,Z,RX,RY,RZ。X,Y,Z表示的是位置坐标，RX,RY,RZ表示的旋转向量。为了便于转换矩阵的计算，需要将这个6个值转换成描述矩阵的形式:

$$H = \begin{bmatrix}R & T\\\\0 &1\end{bmatrix}$$

其中$R$为旋转矩阵($3\times3$)，$T$为平移向量($3\times1$)。
旋转矩阵由旋转向量经罗德里格斯变换可以转换而成。在opencv中直接使用rodrigues函数就可以进行转换。

像素坐标系到相机坐标系转换矩阵($H_{pc}$)

简单来说就是将图像像素坐标上的点转换到相机坐标系。

图像像素坐标： 图像像素坐标系是以左上角为零点，水平向右为x正方向，垂直向下为y正方向，如下图所示：

所以像素坐标系与相机坐标系之间的转换关系其实就是计算相机的内部参数矩阵，而这部分是需要通过标定板来进行标定的。关于相机标定，opencv官方就已经由一些解释，同时在官方github中也有了calibrate的例子，参考这些就可以把内部参数求解出来。当我们使用相机标定矩阵时，注意标定板应该在固定位置保持不变，使机器人在大概12个不同的位置角度对其进行拍摄。

这里$H_{pc}$是相机内部参数矩阵的增广矩阵:

$$H_{pc} = \begin{bmatrix} cameraMatrix \mid 0\end{bmatrix}_{3 \times 4}$$

相机坐标系到工具头坐标系转换矩阵($H_{cg}$)

相机坐标系与工具头坐标系之间的转换就是所谓的手眼转换。（前提是相机与工具头之间的关系是固定的）

手眼标定的主要目的就是标定相机和工具头末端之间的转换矩阵($H_{cg}$)，在上图中为$X$。

求解思路：

为了便于解释，使用如下图：

如图所示，

$C_i$：相机的位置坐标（由opencv中的张氏标定可以算出相机的外部参数矩阵，即为相机的位置）

$G_i$：工具头末端位置坐标（可由机箱直接读到此时的位置信息）

$CW$：标定板坐标系

$RW$: 机器人坐标系

上图表示的是工具头和相机分别在$n$个位置对标定板进行拍摄。

进一步的：

$H_{ci}$：从$CW$到$C_i$的坐标转换

$H_{gi}$：从$G_i$到$RW$的坐标转换

$H_{gij}$：从$G_i$到$G_j$的坐标转换

$H_{cij}$：从$C_i$到$C_j$的坐标转换

$H_{cg}$：从$C_i$到$G_j$的坐标转换

其中：

$$H = \begin{bmatrix}R & T\\\\0 &1\end{bmatrix}$$

$R$为旋转矩阵($3\times3$)，$T$为平移向量($3\times1$)。

因为：

$$\begin{cases} H_{gi}=H_{cg}H_{ci} \\\\ H_{gj}=H_{gij}H_{gi} \\\\ H_{cj}=H_{cij}H_{ci} \end{cases}$$

所以可以得到：

$$H_{gij}H_{cg} = H_{cg}H_{cij}$$

所以实际只要三个位置就可以计算出手眼转换矩阵$H_{cg}$，但因为通常需要10个位置左右才能得到比较准确的得到相机的外部参数矩阵，所以实际上还是需要在10个以上位置拍摄标定板。

求解$H_{cg}$也是比较麻烦的一个部分，这里我参考的是这篇博客中介绍的求解方式。

求解$H_{cg}$的java代码如下：

import org.opencv.core.*;
import org.opencv.imgproc.*;
import java.util.ArrayList;
import org.apache.commons.math3.linear.Array2DRowRealMatrix;
import org.apache.commons.math3.linear.LUDecomposition;
import org.apache.commons.math3.linear.RealMatrix;
import org.apache.commons.math3.analysis.function.Acos;
import org.apache.commons.math3.analysis.function.Sin;
import org.apache.commons.math3.geometry.euclidean.threed.Vector3D;

public class Calculate_Hcg{
  Acos acos;
  Sin sin;
  private ArrayList<double[][]> Hc;//相机描述矩阵
  private ArrayList<double[][]> Hcij;//相机ij位置的转换矩阵
  private ArrayList<double[][]> Hg;//工具描述矩阵
  private ArrayList<double[][]> Hgij;//相机ij位置的转换矩阵
  public ArrayList<double[][]> Hcg;//相机ij位置的转换矩阵
  
  public void hcg(List<Mat> rc_vec,List<Mat> tc_vec,List<Mat> rg_vec,List<Mat> tg_vec){
  //传入的参数分别是图像的旋转和平移向量，工具手的旋转和平移向量
    double[][] hcg_temp;
    get_hcij(rc_vec,tc_vec);
    get_hgij(rg_vec,tg_vec);
    for(int i=0;i<Hgij.size()-1;i++){
      hcg_temp = caluate_Hcg(Hcij.get(i),Hcij.get(i+1),Hgij.get(i),Hgij.get(i+1));
      Hcg.add(hcg_temp);
    }
  }
  
  private Vector3D caluate_k(double[][] data){
    double R[][] = new double[3][3];
    for(int i = 0;i<3;i++){
      for(int j = 0;j<3;j++){
        R[i][j] = data[i][j];
      }
    }
    double w_temp[]= new double[3];
    double trace = R[0][0]+R[1][1]+R[2][2];
    float trace_f = (float) trace;
    double q = acos((trace_f - 1)/2);
    float q_f = (float) q;
    w_temp[0] = q/(2*sin(q_f))*(R[2][1] - R[1][2]);
    w_temp[1] = q/(2*sin(q_f))*(R[0][2] - R[2][0]);
    w_temp[2] = q/(2*sin(q_f))*(R[1][0] - R[0][1]);
    Vector3D w = new Vector3D(w_temp);
   return w;
  }
  
  private RealMatrix vect2mat(Vector3D k1,Vector3D k2,Vector3D k3){  //向量转换成矩阵
    double mat[][] = new double[3][3];
    mat[0][0] =   k1.getX();
    mat[1][0] =   k1.getY();
    mat[2][0] =   k1.getZ();
    mat[0][1] =   k2.getX();
    mat[1][1] =   k2.getY();
    mat[2][1] =   k2.getZ();
    mat[0][2] =   k3.getX();
    mat[1][2] =   k3.getY();
    mat[2][2] =   k3.getZ();
    RealMatrix realmat = new Array2DRowRealMatrix(mat);
    return realmat;
  }
  
  private RealMatrix get_tvec(double[][] Hij){ //得到平移向量
    double tvecs[][] = new double[3][1];
    tvecs[0][0] = Hij[0][3];
    tvecs[1][0] = Hij[1][3];
    tvecs[2][0] = Hij[2][3];
    RealMatrix tvecs_mat = new Array2DRowRealMatrix(tvecs);
    return tvecs_mat;
  }
  
  private RealMatrix matrix_sub(RealMatrix v1,RealMatrix v2){ //矩阵相减
    assert(v1.getColumnDimension()== v2.getColumnDimension());
    assert(v1.getRowDimension()== v2.getRowDimension());
    int row = (int) v1.getRowDimension();
    int col = (int) v1.getColumnDimension();
    double sub_mat[][] = new double[row][col];
    for(int i  = 0;i<row;i++){
      for(int j = 0;j<col;j++){
        sub_mat[i][j] = v1.getData()[i][j] - v2.getData()[i][j];
      }
    }
    RealMatrix sub_realmat = new Array2DRowRealMatrix(sub_mat);
    return sub_realmat;
  }
  
  private RealMatrix doublearr_sub_eye(double[][] H){
    double H_size3[][] = new double[3][3];
    for(int i = 0 ;i<3;i++){
      for(int j = 0;j<3;j++){
        H_size3[i][j] = H[i][j];
      }
    }
    H_size3[0][0] = H_size3[0][0] -1;
    H_size3[1][1] = H_size3[1][1] -1;
    H_size3[2][2] = H_size3[2][2] -1;
    RealMatrix H_mat = new Array2DRowRealMatrix(H_size3);
    return H_mat;
  }
  
  private RealMatrix appendmat(RealMatrix m1,RealMatrix m2){ //两个矩阵append
    int row1 = (int) m1.getRowDimension();
    int row2 = (int) m2.getRowDimension();
    int col1 = (int) m1.getColumnDimension();
    int col2 = (int) m2.getColumnDimension();
    int new_row = row1+row2;
    assert(col1==col2);
    double new_mat[][] = new double[row1+row2][col1];
    for(int i = 0;i<new_row;i++){
      if(i<row1){
        for(int j = 0;j<col1;j++){
          new_mat[i][j] = m1.getData()[i][j];
        }
      }
      else{
        for(int k = 0;k<col1;k++){
          new_mat[i][k] = m2.getData()[i-row1][k];
        }
      }
    }
    RealMatrix H_mat = new Array2DRowRealMatrix(new_mat);
    return H_mat;
  }
  
  private double[][] get_hcg(RealMatrix R,RealMatrix t){ 
    double Hcg[][] = new double[4][4];
    for(int i = 0;i<3;i++){
      for (int j = 0;j<4;j++){
        if(j<3){
          Hcg[i][j] = R.getData()[i][j];
        }
        else{
          Hcg[i][j] = t.getData()[i][0];
        }
      }
    }
    Hcg[3][0] = 0;
    Hcg[3][1] = 0;
    Hcg[3][2] = 0;
    Hcg[3][3] = 1;
    return Hcg;
  }
  
  private double[][] caluate_Hcg(double[][] hcij1,double[][] hcij2,double[][] hgij1,double[][] hgij2){
    Vector3D kc1 = caluate_k(hcij1);  //3x1列向量
    Vector3D kc2 = caluate_k(hcij2);
    Vector3D kd1 = caluate_k(hgij1);
    Vector3D kd2 = caluate_k(hgij2);
    Vector3D kc3 = Vector3D.crossProduct(kc1,kc2); //1x3
    Vector3D kd3 = Vector3D.crossProduct(kd1,kd2);
    RealMatrix a_temp = vect2mat(kc1,kc2,kc3);
    RealMatrix b_temp = vect2mat(kd1,kd2,kd3);
    RealMatrix R = a_temp.multiply(inverseMatrix(b_temp));  //  旋转矩阵3x3
    RealMatrix tc1 = get_tvec(hcij1);
    RealMatrix tc2 = get_tvec(hcij2);
    RealMatrix td1 = get_tvec(hgij1);
    RealMatrix td2 = get_tvec(hgij2);
    RealMatrix c = matrix_sub(R.multiply(td1),tc1); //3X1
    RealMatrix d = matrix_sub(R.multiply(td2),tc2);
    RealMatrix a = doublearr_sub_eye(hcij1);  //3x3
    RealMatrix b = doublearr_sub_eye(hcij2);
    RealMatrix h = appendmat(a,b);
    RealMatrix y = appendmat(c,d);
    RealMatrix t = inverseMatrix(h.transpose().multiply(h)).multiply(h.transpose()).multiply(y); //平移向量3x1
    double[][] Hcg = get_hcg(R,t);
    return Hcg;
  }
  
  private void get_hcij(List<Mat> rc_vec,List<Mat> tc_vec){
    double[][] h_temp;//存放描述矩阵的临时值
    RealMatrix hcij;//计算ij矩阵
    Hc = new ArrayList<double[][]>();  //相机的描述矩阵
    Hcij = new ArrayList<double[][]>(); //相机ij位置的转换矩阵
    for(int i=0;i<rc_vec.size();i++){
      h_temp = getH(rc_vec.get(i),tc_vec.get(i));//4x4的数组,double[][]类型
     // double htoarray[][]=h_temp.getData();//转换成数组
      Hc.add(h_temp);
    }
    for(int j = 0;j<rc_vec.size()-1;j++){
     // double[][] b = Hc.get(j);  //还需要将数组转换成矩阵的形式
      RealMatrix mat1 = new Array2DRowRealMatrix(Hc.get(j));//还需要将数组转换成矩阵的形式
      RealMatrix mat2 = new Array2DRowRealMatrix(Hc.get(j+1));
      hcij = mat1.multiply(inverseMatrix(mat2)); //matrix格式
      double hcijtoarray[][]=hcij.getData();//转换成数组
      Hcij.add(hcijtoarray);
    }
  }
  
  private void get_hgij(List<Mat> rg_vec,List<Mat> tg_vec){
    double[][] h_temp;//存放描述矩阵的临时值
    RealMatrix hgij;//计算ij矩阵
    Hg = new ArrayList<double[][]>();  //机械臂的描述矩阵
    Hgij = new ArrayList<double[][]>(); //机械臂ij位置的转换矩阵
    for(int i=0;i<rg_vec.size();i++){
      h_temp = getH(rg_vec.get(i),tg_vec.get(i));//4x4的数组,double[][]类型
      Hg.add(h_temp);
    }
    for(int j = 0;j<rg_vec.size()-1;j++){
     // double[][] b = Hc.get(j);  //还需要将数组转换成矩阵的形式
      RealMatrix mat1 = new Array2DRowRealMatrix(Hg.get(j));//还需要将数组转换成矩阵的形式
      RealMatrix mat2 = new Array2DRowRealMatrix(Hg.get(j+1));
      hgij = inverseMatrix(mat1).multiply(mat2); //matrix格式
      double hgijtoarray[][]=hgij.getData();//转换成数组
      Hgij.add(hgijtoarray);
    }
  }
  

  private double[][] getH(Mat rvecs,Mat tvecs) {//将旋转向量和平移向量转换成矩阵
    Mat rota_mat = new Mat(3, 3, CvType.CV_32FC1);
    double [] result;
    Calib3d.Rodrigues(rvecs,rota_mat);
    double exterarr[][] = new double[4][4];
    for(int i = 0;i<3;i++){
      for (int j = 0;j<4;j++){
        if(j<3){
          result = rota_mat.get(i,j);
          exterarr[i][j] = result[0];
        }
        else{
            exterarr[i][j] = tvecs.get(i,0)[0];
        }
      }
    }
    exterarr[3][3] = 1.0;  
    //extermat = new Array2DRowRealMatrix(exterarr);
    return exterarr;
  }
  
  private RealMatrix inverseMatrix(RealMatrix A) {//求逆矩阵
    RealMatrix result = new LUDecomposition(A).getSolver().getInverse();
    return result; 
  }
}

2.1.2 像素坐标转换到世界坐标

得到前面三个转换矩阵后，就可以通过下面的公式将图像上的点$(u,v)$转换成世界坐标下的点$(x,y,z)$（注意：高度$z$是给定的）：

$$z \begin{bmatrix}u\\\\v\\\\1\end{bmatrix} = H_{pc}H_{cg}H^{-1}_{rg} \begin{bmatrix}x\\\\y\\\\z\\\\1\end{bmatrix}$$

设：

$$H_{pc}H_{cg}H^{-1}_{rg} = \begin{bmatrix}a_0&b_0&c_0&d_0\\\\a_1&b_1&c_1&d_1\\\\a_2&b_2&c_2&d_2\\\\a_3&b_3&c_3&d_3 \end{bmatrix}$$

则：

$$\begin{bmatrix} x \\\\y \end{bmatrix} = \begin{bmatrix} ua_2 - a_0 &ub_2 - b_0 \\\\va_2 - a_1 &vb_2-b_1 \end{bmatrix}^{-1}\begin{bmatrix} d_0-ud_2-(uc_2-c_0)z \\\\d_1-vd_2-(vc_2-c_1)z \end{bmatrix}$$

这样就把图像上的点转换到了机器人坐标系下的点。

2.2 瓷砖特征信息提取

图像算法

---

• 输入：

  图片src

• 输出过程

  1. 对图像src预处理（高斯模糊、开操作），及canny边缘检测，得到处理后的图像img_canny

  2. 对img_canny进行轮廓检测，得到轮廓点集contours

  3. 根据各轮廓面积，对轮廓进行过滤筛选，对保留下的轮廓点集由Hu矩计算得到各轮廓质心

  4. 根据轮廓质心得到edge_tile_flag，同时将轮廓点集区分为左右点集（分别表示吸取的和地面的瓷砖）points_left,points_right

  5. 对points_left,points_right使用最大距离法计算出轮廓的拐点corner_left,corner_right

  6. 由corner_left,corner_right筛选出points_left,points_right中的边缘直线点集line_left,line_right，并由PCA最小二乘法拟合直线

• 输出

  line_left,line_right,corner_left,corner_right

---

2.2.1 图像预处理

特征信息最关键的地方就在边缘检测，目前使用的是canny边缘检测算法,opencv中可以直接使用canny函数（在写这篇文章时，其实已经发现了一种效果更好的边缘检测算法-Unsupervised Smooth Contour Detection，但还时间将其应用在图像识别算法中，之后会再整理）。

private Mat preprocess_image(Mat img){ //图像预处理
    Size size = new Size(3,3); //模糊图像用的核函数的尺寸大小
    Size size2 = new Size(5,5); //形态学转换的核函数的尺寸大小
    Mat img_canny = new Mat(); //存储canny边缘检测后的图片
    Mat img_gray = new Mat();//存储灰度图
    Imgproc.cvtColor(img,img_gray,Imgproc.COLOR_BGR2GRAY); //转换成灰度图
    Imgproc.blur(img_gray,img_gray,size);   //图像平滑
    Mat element;
    element = Imgproc.getStructuringElement(Imgproc.MORPH_RECT,size2);
    Imgproc.morphologyEx(img_gray,img_gray,1,element); //形态学转换  1：开操作
    Imgproc.Canny(img_gray,img_canny,g_nThresh,g_nThresh*2); //canny边缘检测
    return img_canny;
  }

2.2.2 轮廓检测

在canny边缘检测算法之后由findcontours可以得到其检测到的所有边缘轮廓的点集，接下来利用opencv的minAreaRect函数可以算出轮廓的最小外接矩形。

private void cnt_info(List<MatOfPoint> contours){ //获得详细的边缘轮廓信息
    boxcontours_list = new ArrayList<org.opencv.core.Point[]>(); //轮廓外接矩形的四个定点
    area_list = new ArrayList<Double>();  //外接矩形面积
    rect_list = new ArrayList<RotatedRect>(); //外接矩形
    contours_appro = new ArrayList<MatOfPoint>();
    box_appro = new ArrayList<org.opencv.core.Point[]>();
    for(int i = 0;i< contours.size();i++){
       MatOfPoint cnt = contours.get(i);
       MatOfPoint2f  newcnt = new MatOfPoint2f(cnt.toArray()); //将MatOfPoint转换成MatOfPoint2f
       RotatedRect rect = Imgproc.minAreaRect(newcnt);
       Size size_area = rect.size;
       double area = size_area.area();
       org.opencv.core.Point vertices[] = new org.opencv.core.Point[4];//定义四个顶点
       rect.points(vertices); //将rect中的定点赋值给vertices
       boxcontours_list.add(vertices); //将四个顶点存入list中
       area_list.add(area);
       rect_list.add(rect);
     }
  }

2.2.3 轮廓筛选与质心计算

接下来可以先根据轮廓面积过滤掉一些面积小于某一阈值的轮廓。

//java
private ArrayList<Integer> get_indexarea(List<MatOfPoint> contours,List<Double> area_list){ //根据轮廓面积进行筛选
    ArrayList<Integer> index_area_appro = new ArrayList<Integer>();
    ArrayList<Integer> index_area_list = new ArrayList<Integer>();
    try{
      List<Double> area_list_temp = deepCopy(area_list); //深拷贝
      int len = area_list.size(); //获得此时寻找到的轮廓列表的大小 这里是可以保证len > 2的
      int index_area;
      Collections.sort(area_list);  //先升序再降序
      Collections.reverse(area_list);
      if(len < 4){
        for(int i = 0;i < len;i++){
          Double area = area_list.get(i);
          if(area > 5000){
            index_area = area_list_temp.indexOf(area);
            index_area_list.add(index_area);
          }
        }
      }
      else{
        for(int i = 0;i < 4;i++){
          Double area = area_list.get(i);
          if(area > 5000){
            index_area = area_list_temp.indexOf(area);
            index_area_list.add(index_area);
          }
        }
      }
    }catch (Exception e){
       e.printStackTrace();  
     }
   if(index_area_list.size() == 0){
      int error = -1;
      index_area_appro.add(error);
      return index_area_appro;
    }
    else{
      index_area_appro = GetCenterPoint(contours,index_area_list);    
      return index_area_appro;
    }
  }

在上面函数可以看到还有一个函数GetCenterPoint(contours,index_area_list)，根据得到的轮廓面积，可以由moments函数得到轮廓Hu矩，并由Hu矩得到轮廓的质心。

2.2.4 edge_tile_flag

瓷砖主要会以以下三种情况出现在画面中：

所以由各轮廓质心的相对关系可以确定在图像中那一块瓷砖是被机器人吸取的，哪一块是平面上需要去靠近的。同时，有了这些信息才能便于之后的轮廓直线拟合与机器人的运动控制

private ArrayList<Integer> GetCenterPoint(List<MatOfPoint> contours,ArrayList<Integer> index_area_list){ //计算得到轮廓的重心点,并对其进行分类，得到左右轮廓的索引
     //ArrayList<org.opencv.core.Point> gravity_point = new  ArrayList<org.opencv.core.Point>();
     ArrayList<Integer> index_appro = new ArrayList<Integer>();
     int len = index_area_list.size();
     int max_x = 0;
     int max_y = 0;
     int index_l = 0;
     int index_r = 0;
     if(len == 2){
       //这里需要去判断当瓷砖是某一行的第一块转时的情况
       MatOfPoint cnt1 = contours.get(index_area_list.get(0));
       Moments p1 = Imgproc.moments(cnt1);
       int y1 = (int) (p1.get_m01() / p1.get_m00());
       MatOfPoint cnt2 = contours.get(index_area_list.get(1));
       Moments p2 = Imgproc.moments(cnt2);
       int y2 = (int) (p2.get_m01() / p2.get_m00());
       index_l = (y1 > y2) ? 0:1;
       index_r = 1-index_l;
       MatOfPoint cnt_r = contours.get(index_area_list.get(index_r));
       MatOfPoint cnt_l = contours.get(index_area_list.get(index_l));
       Moments p_r = Imgproc.moments(cnt_r);
       Moments p_l = Imgproc.moments(cnt_l);
       int x_r = (int) (p_r.get_m10() / p_r.get_m00());
       int x_l = (int) (p_l.get_m10() / p_l.get_m00());
       if(x_r > x_l){
         edge_tile_flag = 0;
       }
       else{
         edge_tile_flag = 1;//说明此时的位于每行的第一个
       }
     }
     else{
       edge_tile_flag = 0;
       for(int i = 0 ; i < len ; i ++){
         MatOfPoint cnt = contours.get(index_area_list.get(i));
         Moments p = Imgproc.moments(cnt);
         int x = (int) (p.get_m10() / p.get_m00());
         int y = (int) (p.get_m01() / p.get_m00());
         if( y > max_y){
           max_y = y;
           index_l = i;
         }
         if( x > max_x){
           max_x = x;
           index_r = i;
         }
       }
     }
     index_appro.add(index_area_list.get(index_l));
     index_appro.add(index_area_list.get(index_r));
     return index_appro;
  }

edge_tile_flag变量表示的是一个标记，主要用来标记此时瓷砖是否为每行的首列。因为如果瓷砖在首列时所用的图像算法是不一样的。
对于前面的三种形式：

edge_tile_flag分别为0,1,0，1,0和分别对应如下的贴砖策略：

一类是瓷砖放置位置在首列，另一种是瓷砖放置位置非首列。通过图像识别算法可以判断出当前属于哪一种类型，但是当需要瓷砖与瓷砖之间保持一定的间隙时，需要知道往哪一个方向保持间隙，所以需要知道当前位置的类型。

瓷砖放置位置在首列的情况：

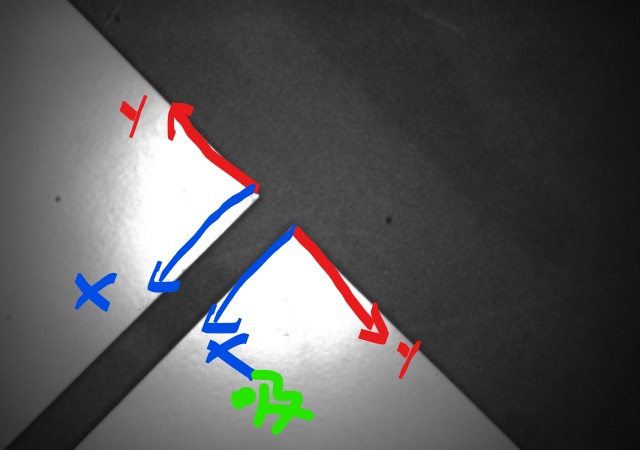
这种情况下，瓷砖与瓷砖之间应该在y方向下保持特定间隙，x方向应该尽量减小间隙。

瓷砖放置位置在非首列的情况：

在非首列情况下，瓷砖与瓷砖之间应该在x方向下保持特定间隙，y方向应该尽量减小间隙。

有了以上这些信息,就可以将合适的轮廓点集以及各轮廓的最小外接矩形的四个角点信息进行保存输出：

private Mat get_contours_info(Mat g_srcimg){ //获得轮廓信息的函数
    List<MatOfPoint> contours = new ArrayList<MatOfPoint>();//保存轮廓的点集
    Mat hierarchy = new Mat();
    Mat img_canny = preprocess_image(g_srcimg); //图像预处理
    Imgproc.findContours(img_canny,contours,hierarchy,1,2); //寻找轮廓
    if(contours.size() < 2){
      double neg = -1;
      rate.add(neg);
    }
    else{
      cnt_info(contours);
      double rate1,rate2;
        index_area_appro = get_indexarea(contours,area_list); //这里面是合适的轮廓的索引
        if(index_area_appro.get(0) == -1){
          double neg = -1;
          rate.add(neg);
        }
        else{
          RotatedRect rect_max_temp = rect_list.get(index_area_appro.get(0));
          RotatedRect rect_max_sec_temp = rect_list.get(index_area_appro.get(1));
          if((rect_max_temp.size.width == 0) | (rect_max_temp.size.height == 0)){
            rate1 = 100;
          }
          else{
            rate1 = max_value(rect_max_temp.size.width / rect_max_temp.size.height,rect_max_temp.size.height / rect_max_temp.size.width); //返回两个数中的较大值
          }
          if((rect_max_sec_temp.size.width == 0) | (rect_max_sec_temp.size.height == 0)){
            rate2 = 100;
          }
          else{
            rate2 = max_value(rect_max_sec_temp.size.width / rect_max_sec_temp.size.height,rect_max_sec_temp.size.height / rect_max_sec_temp.size.width); //返回两个数中的较大值
         }
         rate.add(rate1);
         rate.add(rate2);
         contours_appro.add(contours.get(index_area_appro.get(0)));
         contours_appro.add(contours.get(index_area_appro.get(1)));
         box_appro.add(boxcontours_list.get(index_area_appro.get(0)));
         box_appro.add(boxcontours_list.get(index_area_appro.get(1)));  
        } 
    }
    return img_canny;
  }

由之前的代码可以看出来，提取轮廓特征信息只使用两个轮廓点集即可。

2.2.5 最大距离法

得到合适的轮廓点集之后，就可以计算瓷砖的角点，这里使用最大距离法计算瓷砖的角点。最大距离法的主要思想是，对于一条折现，先找出整个点集的首尾两个点，然后找到整个点集中距离首尾两点连线的距离最大的点。

private void get_cornerpoints(){ //使用最大距离法，获得轮廓点集的拐点
    points_left = contours_appro.get(0).toList();
    points_right = contours_appro.get(1).toList();
    Double points_left_arr[][] = get_points_array(points_left); //转换成数组，用来进行排序
    Double points_right_arr[][] = get_points_array(points_right);
    sort(points_left_arr, new int[] {0,1}); //按横坐标升序
    sort(points_right_arr, new int[] {0,1});
    int len_left = points_left_arr.length;
    int len_right = points_right_arr.length;
    org.opencv.core.Point pointl_1 = new org.opencv.core.Point(points_left_arr[0][0],points_left_arr[0][1]);// 按横坐标升序，得到第一个点坐标，记为轮廓1的第一个参考点
    org.opencv.core.Point pointl_2 = new org.opencv.core.Point(points_left_arr[len_left-1][0],points_left_arr[len_left-1][1]); //继续按横坐标升序，取最后一个点集，作为第二个参考点
    sort(points_left_arr, new int[] {1,0}); //按纵坐标升序
    sort(points_right_arr, new int[] {1,0});
    org.opencv.core.Point pointr_1 = new org.opencv.core.Point(points_right_arr[0][0],points_right_arr[0][1]);
    org.opencv.core.Point pointr_2 = new org.opencv.core.Point(points_right_arr[len_right-1][0],points_right_arr[len_right-1][1]);
    
    if((pointl_2.x - pointl_1.x) == 0){ //垂直直线
      corner_point_left.x = 0;
      corner_point_left.y = 0;
    }
    else{
      double k1 = (pointl_2.y - pointl_1.y) / (pointl_2.x - pointl_1.x);
      double b1 = pointl_2.y - k1 * pointl_2.x;
      int index1 = calculate_distance(points_left,k1,b1);
      corner_point_left.x = points_left.get(index1).x;
      corner_point_left.y = points_left.get(index1).y;
    }
    if((pointr_2.x - pointr_1.x) == 0){
      double b2 = pointr_1.x;
      int index2 = calculate_distance_infinate(points_right,b2);
      corner_point_right.x = points_right.get(index2).x;
      corner_point_right.y = points_right.get(index2).y;
    }
    else{
      double k2 = (pointr_2.y - pointr_1.y) / (pointr_2.x - pointr_1.x);
      double b2 = pointr_2.y - k2 * pointr_2.x;
      int index2 = calculate_distance(points_right,k2,b2);
      corner_point_right.x = points_right.get(index2).x;
      corner_point_right.y = points_right.get(index2).y;
    }
    corner_point.add(corner_point_left);
    corner_point.add(corner_point_right);
  }  
  
  private int calculate_distance(List<org.opencv.core.Point> points,double k,double b){ //计算到某一直线最大距离的点
    double max = 0;
    int index = 0;
    for(int i = 0;i < points.size();i++){
      double d = FastMath.abs(points.get(i).x * k - points.get(i).y + b);
      if(d > max){
        max = d;
        index = i;
      }
    }
    return index;
  }

  int calculate_distance_infinate(List<org.opencv.core.Point> points,double b){ //计算到斜率为无穷大直线最大距离的点
    double max = 0;
    int index = 0;
    for(int i = 0;i < points.size();i++){
      double d = FastMath.abs(points.get(i).x - b);
      if(d > max){
        max = d;
        index = i;
      }
    }
    return index;
  }

2.2.6 点集筛选

得到角点信息后，两个瓷砖可以进行靠近，但是再靠近之前还需要将两块瓷砖调整至平行，实际上调整平行是再瓷砖靠近之前进行的，但是在这里，为了得到合适的边缘直线的直线方程，需要由角点对轮廓点集进行筛选，仅保留有用的轮廓点集,然后有该点集拟合边缘直线，以获得直线角度。

private List<org.opencv.core.Point> roi_points_r(List<org.opencv.core.Point> points){ //得到新的点集
    List<org.opencv.core.Point> points_new = new ArrayList<org.opencv.core.Point>();
    if(points.size() > 0){
      if(edge_tile_flag == 0){  //需要判断是否是该行的第一块瓷砖
        for(int i = 0 ;i<points.size();i++){
          if(points.get(i).y > corner_point_right.y + 5){
            points_new.add(points.get(i));
          }
        }
      }
      else{
        for(int i = 0 ;i<points.size();i++){
          if(points.get(i).y < corner_point_right.y - 5){
            points_new.add(points.get(i));
          }
        }
      
      }      
    }
    else{
      points_new = points;
    }
     return points_new;
  }
  
  private List<org.opencv.core.Point> roi_points_l(List<org.opencv.core.Point> points){ //得到新的点集
    List<org.opencv.core.Point> points_new = new ArrayList<org.opencv.core.Point>();
    if(points.size() > 0){
      for(int i = 0 ;i<points.size();i++){
        if(points.get(i).x > corner_point_left.x + 5){
          points_new.add(points.get(i));
        }
      }
    }
    else{
      points_new = points;
    }
     return points_new;
  }

这里的roi_points_r和roi_points_l分别表示的地面放置瓷砖的轮廓点集和机器人吸取末端瓷砖的点集。
从代码中可以看出来点集为roi_points_r时，当点集的纵坐标大于角点坐标的纵坐标时保留；点集为roi_points_l时，当点集的横坐标大于角点坐标的横坐标时保留。

2.2.7 基于PCA的最小二乘方式

对于保留的点集接下来既可以进行直线的拟合，这里使用的时基于PCA的最小二乘方式，之所以采用这种算法，可以参考这里，简单的解释如下：

对于当x被认为是没有误差时的单变量输入的点集时，最小二乘是没有问题的（即使是数据扰动很大的斜椭圆情况）。当变量是两个的情况下，例如由平面点集拟合直线时，由于x和y都可能存在误差，故pca法得到更佳的拟合效果

代码如下：

private List<Double> least_square_pca(List<org.opencv.core.Point> points){//PCA最小
    List<Double> Theta = new ArrayList<Double>();
    int len = points.size();
    double k_infinite = 99999999; //表示无穷大的斜率
    double data [][] = new double[len][2];
    double sum_x = 0;
    double sum_y = 0;
    for(int i = 0 ; i< len;i++){
      data[i][0] = points.get(i).x;
      data[i][1] = points.get(i).y;
      sum_x = sum_x + points.get(i).x;
      sum_y = sum_y + points.get(i).y;
    }
    for(int i = 0;i<len;i++){
      data[i][0] = data[i][0] - sum_x/len;
      data[i][1] = data[i][1] - sum_y/len;
    }
    RealMatrix data_matrix = new Array2DRowRealMatrix(data);
    RealMatrix datamatrix2 = data_matrix.transpose().multiply(data_matrix);
    RealMatrix u = new SingularValueDecomposition(datamatrix2).getU();
    RealMatrix n = u.getColumnMatrix(1);
    double n_arr[][] = n.getData();
    if(n_arr[1][0] == 0){
      Theta.add(points.get(0).x);
      Theta.add(k_infinite);
    }
    else{
      double k2 = -n_arr[0][0] / n_arr[1][0];
      double b2 = sum_y / len - k2 * sum_x / len;
      Theta.add(b2); //直线方程的截距
      Theta.add(k2); //直线方程的斜率
    }
    return Theta;
  }

直线拟合之后就可以计算出两条直线的角度及其偏差。